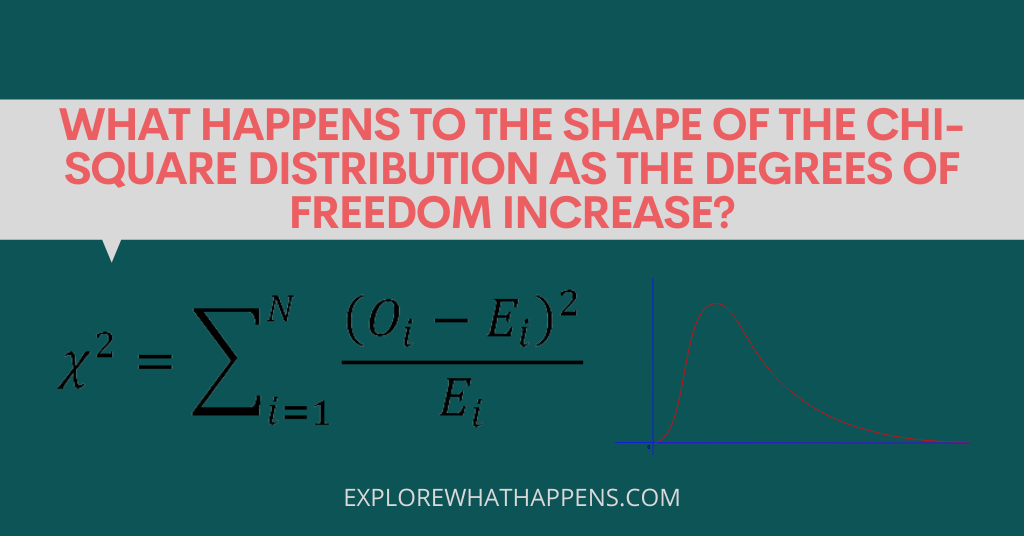
The chi-square distribution is a common probability distribution that is used to determine the likelihood of events. As the degrees of freedom (or a number of observations) increase, the chi-square distribution becomes more heavily skewed towards the left. This means that it will have a smaller probability of occurring at the observed values, and will be more likely to occur at values closer to 0 or 1.
When we have a Chi-squared test, we want to test whether the two samples come from the same distribution. If the values are distributed normally, the probability that the difference between the means of the samples is greater than or equal to the observed difference is 1/2. However, when the number of observations per group is small, the probability that the difference is greater than or equal to the observed difference decreases.
The number of degrees of freedom is the number of observations minus the number of groups. The larger the number of degrees of freedom, the smaller the probability that the difference is greater than or equal to the observed difference.
Therefore, if we have three groups of observations and we want to test the probability that the difference between the means is at least 5 units, we should calculate the chi-square distribution with 3 degrees of freedom. If we have five groups, we should calculate the chi-square distribution with 4 degrees of freedom. And if we have 10 groups, we should calculate the chi-square distribution with 6 degrees of freedom.
What is a chi-square distribution?
A chi-square distribution is a statistical measure used to analyze the differences between observed and expected values. It is often used to test whether or not two groups are statistically different from one another. The chi-square distribution is also used to calculate the p-value for a given test statistic.
When does the chi-square distribution become a normal distribution?
When the number of degrees of freedom (df) is large, the chi-square distribution becomes approximately normal. This occurs because the chi-square distribution is a special case of the gamma distribution, and the gamma distribution is a special case of the normal distribution.
What is the significance of the chi-square distribution?
Chi-squared (χ2) distributions are commonly used to test for normality. Normality is a statistical concept used to describe the frequency distribution of data that resembles a bell-shaped curve. The normal distribution has four parameters: mean, variance, standard deviation, and degrees of freedom. The first three are simple statistics that are used to summarize the data, while the last describes the shape of the curve. If the data is assumed to be normally distributed, the following tests will be valid:
1. Pearson’s Chi-Square Test
The most basic way to assess whether a sample distribution is normal is by using the Pearson Chi-Square Test. This test will indicate whether the observed distribution deviates significantly from the expected value (assuming a normal distribution).
2. Kolmogorov-Smirnov Test
The Kolmogorov-Smirnov (K-S) test is based on the probability that two samples drawn from the same population have the same shape. If the sample does not follow the expected distribution, the K-S test will show significant difference.
3. Shapiro-Wilk Test
The Shapiro-Wilk test is an extension of the K-S test. It examines the ability of the sample to approximate a normal distribution. If the distribution does not follow a normal distribution, the Shapiro-Wilk test will fail.
4. Anderson-Darling Test
The Anderson-Darling (A-D) test is a nonparametric method that does not assume normality.